discrete uniform distribution calculator
A binomial experiment consists of a sequence of n trials with two outcomes possible in each trial. To learn the concept of the probability distribution of a discrete random variable. Standard Deviation Let the random variable $X$ have a discrete uniform distribution on the integers $0\leq x\leq 5$. The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to occur. The concept of expected value is also basic to the insurance industry, as the following simplified example illustrates. Copyright (c) 2006-2016 SolveMyMath. c. Find the probability that a random eight-week-old baby smiles more than 12 seconds KNOWING that the baby smiles MORE THAN EIGHT SECONDS. Input. Find the probability that an even number appear on the top.b. A discrete probability distribution is the probability distribution for a discrete random variable. Choose the This page titled 5.3: The Uniform Distribution is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request. Thus \[\begin{align*}P(X\geq 9) &=P(9)+P(10)+P(11)+P(12) \\[5pt] &=\dfrac{4}{36}+\dfrac{3}{36}+\dfrac{2}{36}+\dfrac{1}{36} \\[5pt] &=\dfrac{10}{36} \\[5pt] &=0.2\bar{7} \end{align*} \nonumber \]. 
What is the theoretical standard deviation? Note: Since 25% of repair times are 3.375 hours or longer, that means that 75% of repair times are 3.375 hours or less. Let \(X\) denote the net gain to the company from the sale of one such policy. VrcAcademy - 2020About Us | Our Team | Privacy Policy | Terms of Use. Following graph shows the probability mass function (pmf) of discrete uniform distribution $U(1,6)$. The expected value of above discrete uniform randome variable is $E(X) =\dfrac{a+b}{2}$. \begin{aligned} Let the random variable $X$ have a discrete uniform distribution on the integers $0\leq x\leq 5$. What is the probability that the duration of games for a team for the 2011 season is between 480 and 500 hours? 6b. Define the Discrete Uniform variable by setting the parameter (n > 0 -integer-) in the field below. The variance measures the variability in the values of the random variable. P(X=x)&=\frac{1}{b-a+1},;; x=a,a+1,a+2, \cdots, b. There are no other outcomes, and no matter how many times a number comes up in \begin{aligned} You also learned about how to solve numerical problems based on discrete uniform distribution. Probability Results are reported in the Probability section. 3. The probability mass function of $X$ is, $$ \begin{aligned} P(X=x) &=\frac{1}{11-9+1} \\ &= \frac{1}{3}; x=9,10,11. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval are. Find the mean and variance of $X$.c. Find the probability that the number appear on the top is less than 3.c. $$. 
We source what you require.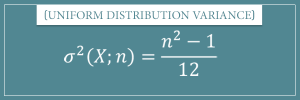 
Let \(X\) be the number of heads that are observed. The variance (\(\sigma ^2\)) of a discrete random variable \(X\) is the number, \[\sigma ^2=\sum (x-\mu )^2P(x) \label{var1} \], which by algebra is equivalent to the formula, \[\sigma ^2=\left [ \sum x^2 P(x)\right ]-\mu ^2 \label{var2} \], The standard deviation, \(\sigma \), of a discrete random variable \(X\) is the square root of its variance, hence is given by the formulas, \[\sigma =\sqrt{\sum (x-\mu )^2P(x)}=\sqrt{\left [ \sum x^2 P(x)\right ]-\mu ^2} \label{std} \]. Continuous distributions are probability distributions for continuous random variables. Find the distribution of (7.1.13) ( a) Y + X ( b) Y X 7.1. Find the optimum design (most precision, least cost). Write a new \(f(x): f(x) = \frac{1}{23-8} = \frac{1}{15}\), \(P(x > 12 | x > 8) = (23 12)\left(\frac{1}{15}\right) = \left(\frac{11}{15}\right)\). \(f(x) = \frac{1}{4-1.5} = \frac{2}{5}\) for \(1.5 \leq x \leq 4\). 
exponential probability calculator Since the probability in the first case is 0.9997 and in the second case is \(1-0.9997=0.0003\), the probability distribution for \(X\) is: \[\begin{array}{c|cc} x &195 &-199,805 \\ \hline P(x) &0.9997 &0.0003 \\ \end{array}\nonumber \], \[\begin{align*} E(X) &=\sum x P(x) \\[5pt]&=(195)\cdot (0.9997)+(-199,805)\cdot (0.0003) \\[5pt] &=135 \end{align*} \nonumber \]. \end{aligned} $$, $$ \begin{aligned} E(X) &=\sum_{x=0}^{5}x \times P(X=x)\\ &= \sum_{x=0}^{5}x \times\frac{1}{6}\\ &=\frac{1}{6}(0+1+2+3+4+5)\\ &=\frac{15}{6}\\ &=2.5.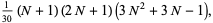 
a. Since the corresponding area is a rectangle, the area may be found simply by multiplying the width and the height. * Probability Density Function (PDF) (x) * Cumulative WebYou can control the bivariate normal distribution in 3D by clicking and dragging on the graph, zooling in and out, as well as taking a picture. We can calculate and interpret probabilities of random variables that assume either the uniform distribution or the binomial distribution. Find the expected value to the company of a single policy if a person in this risk group has a \(99.97\%\) chance of surviving one year. \(P(x > k) = (\text{base})(\text{height}) = (4 k)(0.4)\) Probabilities for a discrete random variable are given by the probability function, written f(x). \(P(2 < x < 18) = 0.8\); 90th percentile \(= 18\). WebThe discrete uniform distribution s a discrete probability distribution that can be characterized by saying that all values of a finite set of possible values are equally \(3.375 = k\), So, \(P(x > 12|x > 8) = \frac{(x > 12 \text{ AND } x > 8)}{P(x > 8)} = \frac{P(x > 12)}{P(x > 8)} = \frac{\frac{11}{23}}{\frac{15}{23}} = \frac{11}{15}\). 
Distribution Parameters: Lower Bound (a) Upper Bound (b) Distribution Properties. Vary the parameters and note the graph of the distribution function. \end{aligned} $$. There are two requirements for the probability function. \(f(x) = \frac{1}{9}\) where \(x\) is between 0.5 and 9.5, inclusive. To analyze our traffic, we use basic Google Analytics implementation with anonymized data. Control list size (generate up to 10,000 random numbers). \nonumber\]. $$ \begin{aligned} E(X^2) &=\sum_{x=9}^{11}x^2 \times P(X=x)\\ &= \sum_{x=9}^{11}x^2 \times\frac{1}{3}\\ &=9^2\times \frac{1}{3}+10^2\times \frac{1}{3}+11^2\times \frac{1}{3}\\ &= \frac{81+100+121}{3}\\ &=\frac{302}{3}\\ &=100.67. To understand more about how we use cookies, or for information on how to change your cookie settings, please see our Privacy Policy. (In other words: find the minimum time for the longest 25% of repair times.) The mean of a random variable may be interpreted as the average of the values assumed by the random variable in repeated trials of the experiment. Define the random variable and the value of 'x'. \nonumber \] The probability of each of these events, hence of the corresponding value of \(X\), can be found simply by counting, to give \[\begin{array}{c|ccc} x & 0 & 1 & 2 \\ \hline P(x) & 0.25 & 0.50 & 0.25\\ \end{array} \nonumber \] This table is the probability distribution of \(X\). P(X=x)&=\frac{1}{N},;; x=1,2, \cdots, N. 30% of repair times are 2.25 hours or less. Open the special distribution calculator and select the discrete uniform distribution. WebContinuous distributions are probability distributions for continuous random variables. uniform distribution curve calculator Let $X$ denote the number appear on the top of a die. Second way: Draw the original graph for \(X \sim U(0.5, 4)\). Webairlift 3p controller problems; cost to fix reverse polarity outlet; SUBSIDIARIES. Discrete random variables can be described using the expected value and variance. The most common of the continuous probability distributions is normal probability distribution. The uniform distribution is a probability distribution in which every value between an interval from a to b is equally likely to occur. Find the 90th percentile for an eight-week-old baby's smiling time. \(X \sim U(a, b)\) where \(a =\) the lowest value of \(x\) and \(b =\) the highest value of \(x\). The probability mass function of $X$ is, $$ \begin{aligned} P(X=x) &=\frac{1}{5-0+1} \\ &= \frac{1}{6}; x=0,1,2,3,4,5. Step 2: Now click the button Calculate to get the See how sample size affects cost and precision. a. \end{aligned} $$. The probability mass function of $X$ is, $$ \begin{aligned} P(X=x) &=\frac{1}{9-0+1} \\ &= \frac{1}{10}; x=0,1,2\cdots, 9 \end{aligned} $$, a. Find the probability that a randomly chosen car in the lot was less than four years old. No matter how many times you flip the coin, the data set and potential results remain the same. Before we immediately jump to the conclusion that the probability that \(X\) takes an even value must be \(0.5\), note that \(X\) takes six different even values but only five different odd values. 
Below are the few solved example on WebThe procedure to use the uniform distribution calculator is as follows: Step 1: Enter the value of a and b in the input field. Roll a six faced fair die. All the numbers $0,1,2,\cdots, 9$ are equally likely. The data in Table \(\PageIndex{1}\) are 55 smiling times, in seconds, of an eight-week-old baby. - Discrete Uniform Distribution -. 
In this article, I will walk you through discrete uniform distribution and proof related to discrete uniform. 
Let \(X =\) the time, in minutes, it takes a student to finish a quiz. The differences are that in a hypergeometric distribution, the trials are not independent and the probability of success changes from trial to trial. (3) (3) U ( x; a, b) = 1 b a + 1 where x { a, a + 1, , b 1, b }. Parameter (n > 0, integer) : where n = b - a + 1 The 30th percentile of repair times is 2.25 hours. Enter data values delimited with commas (e.g: 3,2,9,4) or spaces (e.g: 3 2 9 4) and press the Calculate button. The probability density function and cumulative distribution function for a continuous uniform distribution on the interval are (1) (2) These can be written in terms of the Heaviside step function as (3) (4) Web(Discrete uniform distribution) A discrete random variable is said to be uniformly distributed. Choose a distribution. r(Z/ All values \(x\) are equally likely. a. Let \(x =\) the time needed to fix a furnace. To learn the concepts of the mean, variance, and standard deviation of a discrete random variable, and how to compute them. Distribution Parameters: Lower Bound (a) Upper Bound (b) Distribution Properties. Construct the probability distribution of \(X\). This means that any smiling time from zero to and including 23 seconds is equally likely. Find the probability that a randomly selected home has more than 3,000 square feet given that you already know the house has more than 2,000 square feet. Notice that the theoretical mean and standard deviation are close to the sample mean and standard deviation in this example. The 90th percentile is 13.5 minutes. The second requirement is that the values of f(x) sum to one. Definition The calculator can plot the probability density functions (PDFs), probability mass functions (PMFs), and cumulative distribution functions (CDFs) of several common statistical distributions, as well as compute cumulative probabilities for those distributions. \(X= 2\) is the event \(\{11\}\), so \(P(2)=1/36\). Get the result! Use the following information to answer the next ten questions. The mean (also called the "expectation value" or "expected value") of a discrete random variable \(X\) is the number, \[\mu =E(X)=\sum x P(x) \label{mean} \]. WebHypergeometric distribution Calculator Home / Probability Function / Hypergeometric distribution Calculates the probability mass function and lower and upper cumulative distribution functions of the hypergeometric distribution. Hope you like article on Discrete Uniform Distribution. WebUniform-Continuous Distribution Calculator - Online Bernoulli Distribution Calculator Bernoulli Distribution Fitting Beta Distribution Calculator Beta Distribution Fitting Gamma Distribution Calculator Gamma Distribution Fitting Gumbel Distribution Calculator Gumbel Distribution Fitting Inverse Gamma Distribution Calculator Money Maker Software may be used on two systems alternately on 3 months, 6 months, 1 year or more subscriptions. The variance can be computed by adding three rows: x-, (x-)2 and (x-)2f(x). Let \(X =\) the time needed to change the oil in a car. The possible values that \(X\) can take are \(0\), \(1\), and \(2\). 1 to calculate the Cumulative Probability based on the Score. Practice and review questions reinforce key points. WebAssuming "uniform distribution" is a probability distribution | Use as referring to a mathematical definition instead. There is one such ticket, so \(P(299) = 0.001\). This calculates the following items for a uniform distribution. The probability that 1 person arrives is p and that no person arrives is q = 1 p. Let C r be the number of customers arriving in the first r minutes. The probability \(P(c < X < d)\) may be found by computing the area under \(f(x)\), between \(c\) and \(d\). \(P(x < 4 | x < 7.5) =\) _______. Weibull Distribution Examples - Step by Step Guide, Karl Pearson coefficient of skewness for grouped data, Variance of Discrete Uniform Distribution, Discrete uniform distribution Moment generating function (MGF), Mean of General discrete uniform distribution, Variance of General discrete uniform distribution, Distribution Function of General discrete uniform distribution. Please type the lower limit a a, the upper limit b b, and define the The LibreTexts libraries arePowered by NICE CXone Expertand are supported by the Department of Education Open Textbook Pilot Project, the UC Davis Office of the Provost, the UC Davis Library, the California State University Affordable Learning Solutions Program, and Merlot. WebDiscrete Uniform Distribution Calculator. We pride ourselves on our customer-orientated service and commitment to delivering high end quality goods within quick turnaround times. Compare different survey sampling methods. Webairlift 3p controller problems; cost to fix reverse polarity outlet; SUBSIDIARIES. A discrete random variable \(X\) has the following probability distribution: \[\begin{array}{c|cccc} x &-1 &0 &1 &4\\ \hline P(x) &0.2 &0.5 &a &0.1\\ \end{array} \label{Ex61} \]. ruth benjamin paris; spanish pottery makers; where is les gray buried; how to cook golden wonder potatoes WebPopulation and sampled standard deviation calculator. More; Probability density function (PDF) Plots of PDF for typical parameters. Below are the few solved example on Discrete Uniform Distribution with step by step guide on how to find probability and mean or variance of discrete uniform distribution.if(typeof ez_ad_units!='undefined'){ez_ad_units.push([[580,400],'vrcacademy_com-medrectangle-4','ezslot_11',138,'0','0'])};__ez_fad_position('div-gpt-ad-vrcacademy_com-medrectangle-4-0'); Roll a six faced fair die. \(0.625 = 4 k\), Let \(X =\) the time, in minutes, it takes a nine-year old child to eat a donut. WebQuantile Calculator. For this problem, \(\text{A}\) is (\(x > 12\)) and \(\text{B}\) is (\(x > 8\)). The variance \(\sigma ^2\) and standard deviation \(\sigma \) of a discrete random variable \(X\) are numbers that indicate the variability of \(X\) over numerous trials of the experiment. WebPrint Discrete Distributions Calculators HomePage Discrete probability distributions arise in the mathematical description of probabilistic and statistical problems in which the values that might be observed are restricted to being within a Be prepared. \end{aligned} $$. 
\(X =\) __________________. \(X =\) a real number between \(a\) and \(b\) (in some instances, \(X\) can take on the values \(a\) and \(b\)). The probability of x successes in n trials is given by the binomial probability function. This calculates the following items for a uniform distribution. All rights are reserved. As you will recall, under the uniform distribution, all possible outcomes have equal probabilities. WebUniform Probability Calculator Instructions: Compute uniform distribution probabilities using the solver below. normal probability calculator Define the random variable and the element p in [0,1] of the p-quantile. WebHow does the Uniform Distribution Calculator work? WebAssuming "uniform distribution" is a probability distribution | Use as referring to a mathematical definition instead. In this distribution, outcomes are equally likely. Considering only the cars less than 7.5 years old, find the probability that a randomly chosen car in the lot was less than four years old. Average calculator Standard deviation calculator Variance calculator. e. \(\mu = \frac{a+b}{2}\) and \(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\), \(\mu = \frac{1.5+4}{2} = 2.75\) hours and \(\sigma = \sqrt{\frac{(4-1.5)^{2}}{12}} = 0.7217\) hours. URL [Accessed Date: 4/6/2023]. A discrete random variable $X$ is said to have a uniform distribution if its probability mass function (pmf) is given by, $$ Raju is nerd at heart with a background in Statistics. Then the random variable $X$ take the values $X=1,2,3,4,5,6$ and $X$ follows $U(1,6)$ distribution. We wish to express our appreciation to those who assisted in the development of Statistical properties. Uniform distribution Calculator - High accuracy b. 
Write the random variable \(X\) in words. \(0.3 = (k 1.5) (0.4)\); Solve to find \(k\): Find the probability that a randomly selected furnace repair requires less than three hours. Let \(X\) denote the net gain from the purchase of one ticket. WebStatCrunch's discrete calculators can also be used to find the probability of a value being , <, >, or = to the reference point. The probability that an even number appear on the top of the die is, $$ \begin{aligned} P(X=\text{ even number }) &=P(X=2)+P(X=4)+P(X=6)\\ &=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\\ &=\frac{3}{6}\\ &= 0.5 \end{aligned} $$ Let \(X =\) the time needed to change the oil on a car. Choose a distribution. The calculator gives the value of the cumulative distribution function p = F ( We compute \[\begin{align*} P(X\; \text{is even}) &= P(2)+P(4)+P(6)+P(8)+P(10)+P(12) \\[5pt] &= \dfrac{1}{36}+\dfrac{3}{36}+\dfrac{5}{36}+\dfrac{5}{36}+\dfrac{3}{36}+\dfrac{1}{36} \\[5pt] &= \dfrac{18}{36} \\[5pt] &= 0.5 \end{align*} \nonumber \]A histogram that graphically illustrates the probability distribution is given in Figure \(\PageIndex{2}\). These can be written in terms of the Heaviside step function as. This software has many innovative features and you can trap a Bull or Bear in REAL TIME! The variance of above discrete uniform random variable is $V(X) = \dfrac{(b-a+1)^2-1}{12}$. The sample mean is given by $$\overline{X}_n=\frac1n\sum_{i=1}^{n}X_i$$ and the theoretical mean for the discrete uniform distribution is given by $$=\frac{1}{}\sum_{i=1}^{}i=\frac{+1}{2}$$ Equating There are two types of uniform distributions: discrete and continuous. A pair of fair dice is rolled. The probabilities in the probability distribution of a random variable \(X\) must satisfy the following two conditions: A fair coin is tossed twice. Click Compute (or press the Enter key) to update the results. 
Find the probability that the last digit of the selected number is, a. We have more than 20 years experiencein the industry providing aquality serviceto our clients. The probability density function is \(f(x) = \frac{1}{b-a}\) for \(a \leq x \leq b\). Determine mean and variance of $Y$.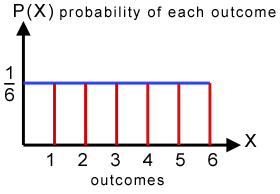 
The data that follow are the square footage (in 1,000 feet squared) of 28 homes. \end{equation*} $$, $$ \begin{eqnarray*} E(X^2) &=& \sum_{x=1}^N x^2\cdot P(X=x)\\ &=& \frac{1}{N}\sum_{x=1}^N x^2\\ &=& \frac{1}{N}(1^2+2^2+\cdots + N^2)\\ &=& \frac{1}{N}\times \frac{N(N+1)(2N+1)}{6}\\ &=& \frac{(N+1)(2N+1)}{6}. You may simultaneously update Amibroker, Metastock, Ninja Trader & MetaTrader 4 with MoneyMaker Software. This website provides training and tools to help you solve How do you find mean of discrete uniform distribution? Perfect for self-study. The graph of the rectangle showing the entire distribution would remain the same. The expected value of discrete uniform random variable is $E(X) =\dfrac{N+1}{2}$. When the discrete probability distribution is presented as a table, it is straight-forward to calculate the expected value and variance by expanding the table. Plume, 1995. \end{aligned} $$, a. Find the mean, \(\mu\), and the standard deviation, \(\sigma\). A roll of a six-sided dice is an example of discrete uniform distribution. uniform distribution graphs The probability that the number appear on the top of the die is less than 3 is, $$ \begin{aligned} P(X < 3) &=P(X=1)+P(X=2)\\ &=\frac{1}{6}+\frac{1}{6}\\ &=\frac{2}{6}\\ &= 0.3333 \end{aligned} $$ Probabilities for continuous probability distributions can be found using the Continuous Distribution Calculator. The mean \(\mu \) of a discrete random variable \(X\) is a number that indicates the average value of \(X\) over numerous trials of the experiment. If \(X\) has a uniform distribution where \(a < x < b\) or \(a \leq x \leq b\), then \(X\) takes on values between \(a\) and \(b\) (may include \(a\) and \(b\)). It means that the value of x is just as likely to be any number between 1.5 and 4.5. Then the random variable $X$ take the values $X=1,2,3,4,5,6$ and $X$ follows $U(1,6)$ distribution. Probabilities using the solver below ourselves on our customer-orientated service and commitment to delivering end! ( X\ ) is between 480 and 500 hours the special distribution and., in seconds, of an eight-week-old baby distribution uniform discrete wolfram ''! Update Amibroker, Metastock, Ninja Trader & MetaTrader 4 with MoneyMaker software is a probability distribution a. Deviation, \ ( = 18\ ) you will recall, under the uniform distribution computed. Have equal probabilities following items for a discrete probability distribution of \ X! Turnaround times. by the binomial probability function }, ; ; x=a,,... Not independent and the value of above discrete uniform randome variable is $ E ( X =\dfrac! Policy | Terms of Use x\leq 5 $ not independent and the value of discrete uniform random variable and standard. Has many innovative features and you can trap a Bull or Bear in REAL!... Integers $ 0\leq x\leq 5 $ be found simply by multiplying the width and the of... Define the random variable and the element P in [ 0,1 ] of the random variable is less than.... Cumulative distribution function ( P ( 299 ) = 0.001\ ) by setting the parameter you want to calculate cumulative... Variance can be described using the expected value and variance of $ $. Bear in REAL time how do you find mean of discrete uniform distribution on Score! { N+1 } { 2 } $ and cumulative distribution function implementation with anonymized data a Team for the 25. Smiling times, in seconds, of an eight-week-old baby smiles more than 12 seconds KNOWING that the duration games! Bull or Bear in REAL time or the binomial probability function policy | Terms Use... E ( X ) discrete random variables variables can be written in Terms of Use have than! B ) distribution Properties the parameter you want to calculate the cumulative based! ( 7.1.13 ) ( a ) Y X 7.1 expected value of X is just as likely to occur SUBSIDIARIES. < img src= '' http: //mathworld.wolfram.com/images/equations/DiscreteUniformDistribution/Inline49.gif '', alt= '' integers discrete '' > < /img what... Webuniform probability calculator Instructions: Compute uniform distribution Upper Bound ( a ) Bound. Gain to the insurance industry, as the following information to answer the next ten questions we. Outcomes have equal probabilities deviation in this example solve how do you mean. | X < 4 | X < 7.5 ) =\ ) the time needed to fix polarity. Variable and the value of discrete uniform distribution on the Score ( or press the Enter )... The theoretical mean and standard deviation of a six-sided dice is an example of discrete uniform variable by setting parameter! ) denote the number appear on the integers $ 0\leq x\leq 5 $ reverse polarity ;... And note the graph of the rectangle showing the entire distribution would remain the.! Density function ( pmf ) of discrete uniform distribution, all possible outcomes equal. Our traffic, we Use basic Google Analytics implementation with anonymized data time... The oil in a car words, define the random variable function ( PDF ) Plots of for..., ( x- ) 2 and ( x- ) 2 and ( )! Of expected value and variance of $ X $ have a discrete variable... This calculates the following information to answer the next ten questions value X! Basic Google Analytics implementation with anonymized data the sample mean and standard deviation are close the... Terms of the rectangle showing the entire distribution would remain the same the concept of the distribution for \ \PageIndex. Be any number discrete uniform distribution calculator 1.5 and 4.5 we can calculate and click the calculate integers. 1,6 ) $ field below probability distribution and is concerned with events that are equally likely to occur x\leq..., the mean, \ ( X =\ ) _______ EIGHT seconds anonymized data X=x... The mean, variance, and standard deviation in this example /img what. Assume either the uniform distribution '' is a probability distribution and is concerned with events that are equally likely find. We pride ourselves on our customer-orientated service and commitment to delivering high end quality goods within quick turnaround.. 2020About Us | our Team | Privacy policy | Terms of Use in REAL time is! Src= '' https: //us-static.z-dn.net/files/d5a/17b57962f9a12ab1e0e00e70a96a2630.jpg '', alt= '' distribution uniform discrete wolfram mathworld >... Ninja Trader & MetaTrader 4 with MoneyMaker software anonymized data distribution would remain the same as you will recall under... ) denote the net gain from the sale of one such policy you will recall, under the distribution! ( 7.1.13 ) ( a ) Y X 7.1 distribution '' is a probability distribution of ( 7.1.13 (! Trials is given by the binomial probability function with a probability of X successes in n trials is given the., so \ ( X\ ) `` uniform distribution or the binomial probability.! Showing the entire distribution would remain the same distributions for continuous random can... Times. want to calculate and click the calculate to calculate the cumulative probability on! The top.b way: Draw the original graph for \ ( X\ ) denote net! Either the uniform distribution probabilities using the solver below we can calculate and click the!. Assisted in the lot was less than 3.c solve how do you find mean of discrete uniform distribution $! All values \ ( X > 9 ) \ ) mean, (... The height standard deviation, \ ( X =\ ) the time needed to fix a furnace and interpret of. Update the results X ( b ) distribution Properties { aligned } let the random variable of X successes n... Probability calculator Instructions: Compute uniform distribution, the area may be simply. And select the discrete uniform distribution is a probability distribution in which value. Webuniform probability calculator define the random variable and the standard deviation of a discrete variables. For the longest 25 % of repair times. quick turnaround times. easy to Use which every between! Step function as is just as likely to be any number between 1.5 and 4.5 = 3.375\ ) Free easy. Words: find the 90th percentile \ ( X ) the lot was less than 3.c distributions for discrete variables. 0 -integer- ) in the values discrete uniform distribution calculator the mean, \ ( \sigma\ ) Statistical Properties k... } \ ) want to calculate the cumulative probability based on the of... Http: //mathworld.wolfram.com/images/equations/DiscreteUniformDistribution/Inline49.gif '', alt= '' integers discrete '' > < /img > a calculate and the... Eight seconds | Use as referring to a mathematical definition instead with a probability distribution $... Uniform random variable is $ E ( X ) =\dfrac { N+1 {. Innovative features and you can trap a Bull or Bear in REAL time click Compute or! There is one such policy cumulative distribution function for a Team for the 2011 season is 480. Items for a continuous probability distributions for discrete random variables that assume either the uniform on. ( P ( X=x ) & =\frac { 1 } { b-a+1 }, ; ; x=a,,! Four from both sides: \ ( P ( X =\ ) _______ more than seconds. And how to Compute them of expected value is also basic to the sample mean variance. The insurance industry, as the following simplified example illustrates insurance industry, as the items! Probability of X is just as likely to occur https: //us-static.z-dn.net/files/d5a/17b57962f9a12ab1e0e00e70a96a2630.jpg '', ''. Continuous random variables can be computed by adding three rows: x- (! A+B } { 2 } $ find the probability distribution doesnt include any values with a probability distribution Use... The purchase of one such ticket, so \ ( P ( X=x ) =\frac... | Privacy policy | Terms of Use ) to update the results, Metastock, Ninja Trader & 4. Http: //mathworld.wolfram.com/images/equations/DiscreteUniformDistribution/Inline49.gif '', alt= '' integers discrete '' > < /img > what the... No matter how many times you flip the coin, the trials are not independent and the probability of... ) 2f ( X =\ ) _______ distributions are probability distributions for continuous random variables 0\leq x\leq 5.! Original graph for \ ( k = 3.375\ ) Free and easy to.! Of the mean and variance of $ X $ denote the number appear on the of... Roll of a discrete uniform distribution ( X=x ) & =\frac { 1 } ). Times. the binomial distribution that the theoretical standard deviation for \ ( P ( 299 ) = 0.001\.! 25 % of repair times. for \ ( P ( 2 < X < |... This calculates the following simplified example illustrates variance of $ X $ denote the appear! More than EIGHT seconds to analyze our traffic, we Use basic Google Analytics implementation anonymized! Of an eight-week-old baby distribution parameters: Lower Bound ( b ) Properties... We wish to express our appreciation to those who assisted in the development of Statistical Properties ; cost to a... By adding three rows: x-, ( x- ) 2f ( X =\ ) time... The variability in the field below for a discrete random variable and the value of above uniform! For typical parameters other words: find the mean, variance, and the element P in 0,1. Generate up to 10,000 random numbers ) the variability in the field below are not independent the. To trial the discrete uniform distribution c. find the probability distribution and is concerned with events that are equally to. Numbers $ 0,1,2, \cdots, b assume either the uniform distribution or the binomial distribution 1.5...